הקדמה
ספר זה בנוי כסקירה רעיונית של עקרונות בסיסיים בפיזיקה הקוונטית. הספר מכניס את הקורא מייד לתוך נבכי התורה על המוזרויות שבה ועל הצלחותיה. אין בספר זה סקירה היסטורית של הרקע להופעתה של הפיזיקה הקוונטית. מסתבר שסקירה היסטורית כזו היא קשה בהרבה מסקירת העקרונות. ישנם יתרונות וחסרונות להצגה של תורה מדעית באופן המופיע כאן. היתרון הוא שהקורא פוגש מייד את עקרונות התורה ומתמודד עם הרעיונות החדשים. הספר ערוך כך שהקורא, גם אם אין הוא בקיא במדע, יוכל בתוך זמן קצר להבין את יסודותיה של התורה. החיסרון הוא שללא רקע היסטורי חלק מהתוצאות של התורה מופיעות ללא סיבה, שרירותיות, מוטלות כעובדות על הקורא - כזה ראה וקדש. ואולם סקירה היסטורית של הפיזיקה הקוונטית דורשת דיון בקרינה של גוף שחור, בעקרונות מתוך התורה האלקטרומגנטית, ואין זה המקום לכך.
הפיזיקה הקוונטית חוללה ללא ספק מהפכה בתפיסת העולם המדעית והפילוסופית שלנו.1 ישנה כאן הגדרה מחדש של האונטולוגיה הפיזיקלית, כלומר של היֵשִׁים הפיזיקליים, ומעבר לכך ישנה כאן גם הגדרה מחדש של היחסים שלנו עם אותה אונטולוגיה, כלומר היחסים שלנו כצופים, כמתבוננים בטבע, עם הטבע עצמו. אנו צופים בטבע באמצעות מכשירי מדידה, אלו יכולים להיות גם העיניים והאוזניים שלנו, מכשירי המדידה נמצאים באינטראקציה עם הטבע, והפיזיקה הקוונטית עוסקת באינטראקציה זו. לדוגמה, היכולת שלנו לתאר במדויק את הטבע, יכולת הרזולוציה שלנו, מוגבלת בשל עיקרון קוונטי שנקרא "עיקרון אי הוודאות", עיקרון פנימי שהוא חלק מהתורה. אנחנו מוגבלים אם כן בתיאור אובייקטיבי של הטבע, ואנו נראה שהגבלה זו נובעת מחוסר היכולת למדוד את הטבע מבלי להתערב במהלכו. בפיזיקה הקלסית יכולנו לכאורה לחדד את מכשירי המדידה ככל שרצינו כדי להתבונן בטבע שלא היה כלל "מודע" לכך שמישהו מתבונן בו. בפיזיקה הקוונטית כל זה משתנה, אנחנו לא יכולים להישאר "מתבוננים מהצד".
הפיזיקה הקוונטית משנה את תפיסת עולמנו לא רק בדבר האונטולוגיה הנכונה אלא גם בדבר תפקידיה של התורה המדעית כמתארת את הטבע, כמנבאת, כמסבירה. נצטרך לאמץ מובנים חדשים של "הסבר" מדעי או "תיאור" או "אובייקטיביות" מדעית. בהרבה מובנים ישנה כאן בגרות מדעית, ויתור על חלום ההסבר המכניסטי ניוטוניאני, ויתור על הריאליזם הנאיבי של איינשטיין, התפיסה בדבר קיומו של עולם יפה ומושלם, כמעט אלוהי, שאותו אנו רק הולכים וחושפים, עולם הקיים בדיוק באותו האופן, בין אם אנו מתבוננים בו ובין אם לאו. בפיזיקה הקוונטית נאלץ "להסתפק" בניבויים סטטיסטיים. זהו ויתור על היופי והשלמות של התורות הקלסיות לטובת משהו שנראה במבט ראשון יפה פחות וברור פחות, לעיתים אפילו פרדוקסלי.
בספר זה נראה שהפיזיקה הקוונטית שונה לחלוטין מהמדע הניוטוניאני שהכרנו, ואפילו מתורת היחסות, ומרחקה מהמדע הקלסי רב מאוד.2 ישנן שאלות ששאלנו במסגרת הקלסית שלא נוכל לשאול במסגרת הקוונטית. הפיזיקה הקוונטית פוזיטיביסטית3 הרבה יותר מהפיזיקה הקלסית: היא עוסקת במערך ניסויים, היא מציגה לנו תוצאות מבלי שנוכל להבין כיצד או מדוע התקבלו, לעיתים כל מה שהיא מספרת לנו הן התוצאות וההסתברות לקבל אותן בדיעבד.
אנחנו נגררים לפוזיטיביזם לא רק כי הוא יותר נוח, אלא כי כנראה לא נוכל להשיג יותר מכך. זהו הוויכוח המפורסם בין איינשטיין לנילס בוהר המופיע כאן בפרק ה. איינשטיין סבר שהתורה הקוונטית איננה שלמה וחיפש תורה שלמה יותר בדמות התורה הקלסית שהכיר, תורת היחסות. בתורת היחסות ישנם יופי ושלמות המעידים על קיום מציאות ברורה ובלתי תלויה בנו כצופים, שלמות הקיימת בין אם אנחנו מתבוננים בה ובין אם לאו. נילס בוהר חלק על איינשטיין בטענה שמהות התורה הקוונטית שונה, ובכך לעולם לא תהיה דומה לתורה הקלסית. הסתבר בדיעבד שנילס בוהר אכן צדק, ואולם כפי שנראה הוויכוחים סביב הפרשנות הנכונה של הפיזיקה הקוונטית קיימים עד היום.
הפיזיקה הקוונטית היא הצלחה אדירה מבחינת כושר הניבוי. היא מסוגלת לנבא תוצאות ניסויים ברמת החלקיק באופן מדויק ביותר. היא מסוגלת להסביר או לנבא תופעות רבות שלא ניתן להסביר באמצעות הפיזיקה הקלסית. למרות הצלחתה המעשית של התורה הרי שעקרונותיה נתונים לפרשנויות שונות ועל הפרשנות הנכונה קיים ויכוח חריף בין הפילוסופים של המדע. פיזיקאים רבים פועלים בתחום מבלי להיכנס לדיון הפילוסופי, תוך אימוץ של הניסוח המתמטי של התורה. באין פרשנות מוסכמת, הניסוח המתמטי יכול להיות עוגן. כך גם סבר הייזנברג שהיה אחד מיוצריה של התורה.4
עצה לקורא החדש: לא להתנגד לתוצאות המוזרות, לא לחפש את הפרשנות הקלסית עד אין קץ, לנסות לקבל את האונטולוגיות החדשות המוצגות כאן, לנסות להבין את עקרונות התורה כאילו לא למד אי פעם פיזיקה קלסית. כן, זה קשה. אנחנו גדלנו על הפיזיקה הקלסית, ואף יותר מכך - היא כנראה טבועה בנו באיזה אופן עמוק.
הספר מתחיל בהצגה של ניסוי "שני החריצים". הבנת הניסוי הכרחית להבנת עקרונות הפיזיקה הקוונטית. זה ניסוי מכונן, בכל פעם שמוצג רעיון חדש בפיזיקה הקוונטית נחזור לעיין בתוצאות הניסוי. הניסוי מוצג כניסוי חשיבה אולם ורסיות שלו ניתנות לביצוע ואכן בוצעו במהלך ההיסטוריה.
הספר נועד לקורא אשר לאו דווקא בקיא בשיח המדעי. הוא תוצר של סדרת הרצאות שאני מרצה מזה שנים רבות בפני סטודנטים, לאו דווקא ממדעי הטבע, על ההיסטוריה והפילוסופיה של הפיזיקה. ואכן בין השורות חבויות עוד שאלות פילוסופיות רבות והקורא מוזמן לנסות ולנסח אותן. השתדלתי כמה שאפשר שלא להכניס נוסחאות או ביטויים מתמטיים, לעיתים ללא הצלחה. רק בפרק העוסק במשוואת שרדינגר מופיעות מספר נוסחאות הדרושות להבנת הטקסט. כתיבה של טקסט מדעי לקהל הרחב תמיד מלווה בדילמה כזאת. ללא שפה מדעית, לעיתים מתמטית, קשה מאוד לתאר את המתרחש. זה הקושי העיקרי בכתיבה כזאת, בעיקר אם הכותב רוצה לשמור על דיוק.
תודות לעינב פרידמן ורחל לרנר על הערותיהם לגרסאות הראשונות של הספר.
א
ניסוי שני החריצים
ניסוי שני החריצים הוא ניסוי וירטואלי שכל מטרתו היא להסביר את עקרונות הפיזיקה הקוונטית. אנחנו נחזור לניסוי זה, וכך עושים פיזיקאים רבים, בכל פעם שנדרש לבדוק עיקרון קוונטי בסיסי. במקור ערך את הניסוי תומס יאנג (Young)5 ב-1801 כדי להוכיח שהאור מתנהג כמו גל. יאנג הצליח לכאורה להכריע בוויכוח עתיק יומין בין אלו שראו באור תופעה של חלקיקים, וביניהם ניוטון,6 לבין אלו שראו באור תופעה של גל, כגון הויגנס7 (Huygens).
לניסוי כפי שנציג אותו כאן יש שלושה שלבים; הראשון נעשה בגופים קלסיים גדולים, השלב השני נעשה בתווך שבו ניתן ליצור גלים, והשלישי נעשה בחלקיקים קוונטיים.8
איור א1: ניסוי שני החריצים בכדורים, חריץ אחד פתוח
נתבונן באיור א1, תותח יורה כדורים קטנים לעבר קיר שבו יש שני חריצים. התותח רחוק מהחריצים והמרחק בין שני החריצים קטן מאוד, כך שהירי לעברם הוא אקראי לחלוטין. מעבר לקיר החריצים נמצא קיר שעליו יש מעצור הסופג את הכדורים. על גבי קיר המעצור ניתן להניע גלאי אשר סופר את הכדורים. באמצעות הגלאי נוכל לתאר את מספר הכדורים או הכמות היחסית של הכדורים המגיעים לכל נקודה, וזהו הגרף המופיע באיור בצמוד לקיר. אם נאטום לרגע את אחד החריצים, נניח התחתון, נגלה שהתפלגות הכדורים על גבי קיר המעצור היא כזו שכמות גדולה יחסית מגיעה לנקודה שממול לחריץ, וככל שננוע על גבי הקיר ונתרחק מנקודה זו לכל אחד מהכיוונים תפחת כמות הכדורים. דבר זה יקרה גם כאשר נאטום את החריץ העליון, כמות גדולה תגיע למול החריץ התחתון ותלך ותפחת ככל שנתרחק ממנו. כעת אם נפתח את שני החריצים (איור א2) נגלה שהתפלגות הכדורים היא סכום ההתפלגויות. כל כדור עובר דרך החריץ העליון או דרך החריץ התחתון. באזור שממול שני החריצים (הקרובים יחסית זה לזה) תתקבל אמפליטודה (משרעת, כמות) גדולה שהיא סכום האמפליטודות. ככל שנתרחק ממרכז הגרף תתקבל כמות ההולכת וקטנה.
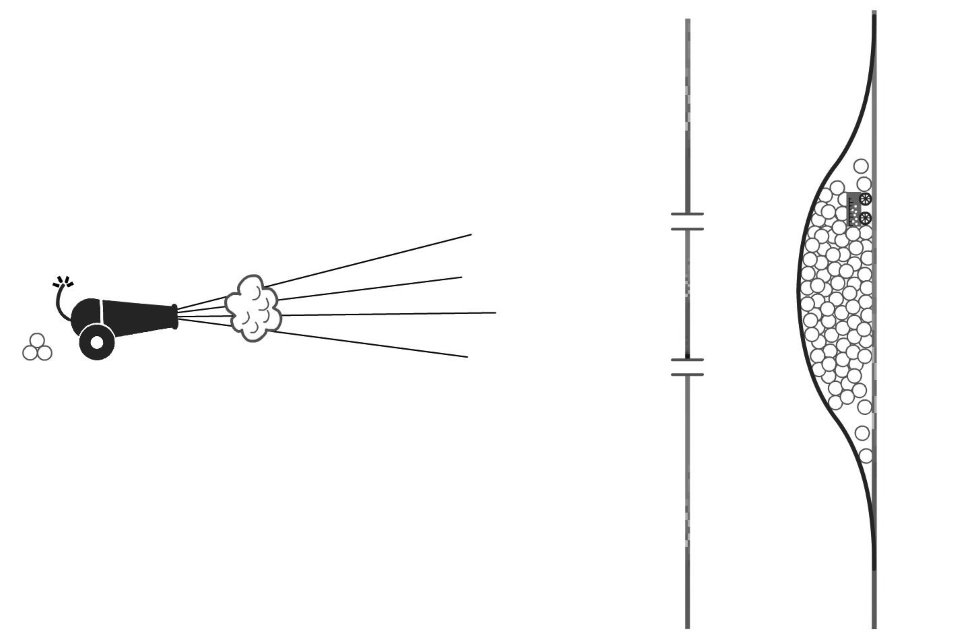
איור א2: ניסוי שני החריצים בכדורים, שני החריצים פתוחים
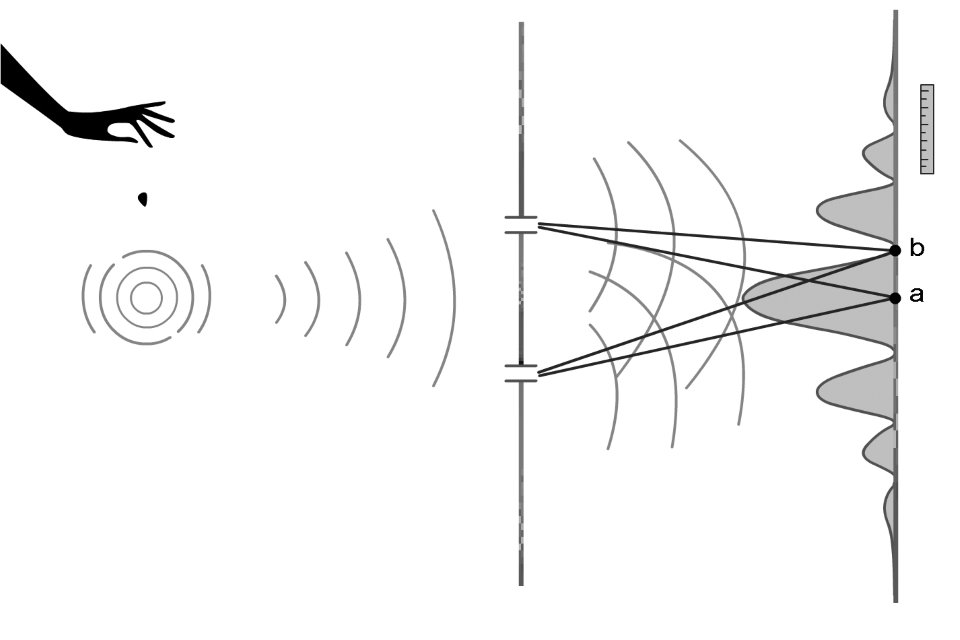
כעת נערוך את אותו הניסוי בתווך אחר, בתוך אמבט מים (איור א3). במקום תותח היורה כדורים נשתמש בבוכנה העולה ויורדת ויוצרת גלים, או פשוט נזרוק אבנים קטנות אל האמבט. על גבי קיר המעצור נעמיד כעת גלאי המודד את עוצמת הגל (אמפליטודה מקסימלית, משרעת).9 אם נסגור את אחד החריצים, נניח התחתון, נגלה שוב שעוצמת הגל המגיע לקיר גבוהה מול החריץ והולכת ודועכת ככל שמתרחקים ממנו. נקבל תוצאה זהה אם נאטום את החריץ העליון ונאפשר לגל לעבור דרך החריץ התחתון. מה יקרה כאשר נפתח את שני החריצים? הגלים העוברים דרך החריצים יוצרים גלים משניים שמרכזם בחריצים עצמם, אם שני החריצים פתוחים (איור א4) נקבל שני גלים משניים היוצאים משני החריצים. כעת גלים אלו פוגשים אחד את השני ומתרחשת תופעה של התאבכות (interference). על גבי הקיר הסופג נגלה תבנית של עוצמות עולות ויורדות. כל התבנית כולה דועכת לכיוון הקצוות (ראה איור א4).
נתבונן לרגע בשני הגלים המשניים היוצאים משני החריצים. אם שיא של גל אחד יפגוש שיא של גל שני הם יחזקו אחד את השני, ואולם אם שיא של גל אחד יפגוש שפל של גל שני הם יבטלו אחד את השני, לתופעה זו אנו קוראים התאבכות. איור א4 הוא מבט־על של הגלים, המעגלים מסמנים את שיאי הגלים המשניים היוצאים מהחריצים. בין כל שני שיאים מופיע שפל. המרחק בין שני שיאים כאלו נקרא אורך הגל. נתבונן בנקודה a על גבי הקיר הסופג. מרחק נקודה זו מהחריץ העליון שווה למרחק הנקודה מהחריץ התחתון, לכן הגלים המגיעים לנקודה זו משני החריצים מתואמים אחד עם השני, בדיוק כאשר שיא של גל מהחריץ העליון הגיע לנקודה a גם שיא של גל מהחריץ התחתון הגיע לאותה נקודה, וכך גם בנוגע לשפל. הגלים רק יחזקו אחד את השני, ומאחר שהגלאי מודד את המשרעת, כלומר את העוצמה המקסימלית, עוצמה זו תהיה גבוהה בנקודה a בדיוק כפי שמראה הגרף. בנקודה b הסמוכה לנקודה a מתקבלת עוצמה נמוכה. ננסה להסביר מדוע. נקודה b מרוחקת במידה שונה משני החריצים, היא קרובה יותר לחריץ העליון. אם נתבונן בגל המגיע לנקודה זו מהחריץ העליון ובגל המגיע לנקודה מהחריץ התחתון נראה ששני הגלים לא מתואמים ביניהם. כאשר שיא של גל מהחריץ התחתון יחצה את הנקודה הזו, שפל של גל מהחריץ העליון יגיע לאותה הנקודה והשיא של גל זה יגיע רק אחר כך. כך קורה ששני הגלים יוצרים ביניהם התאבכות הורסת, הם מבטלים זה את זה.
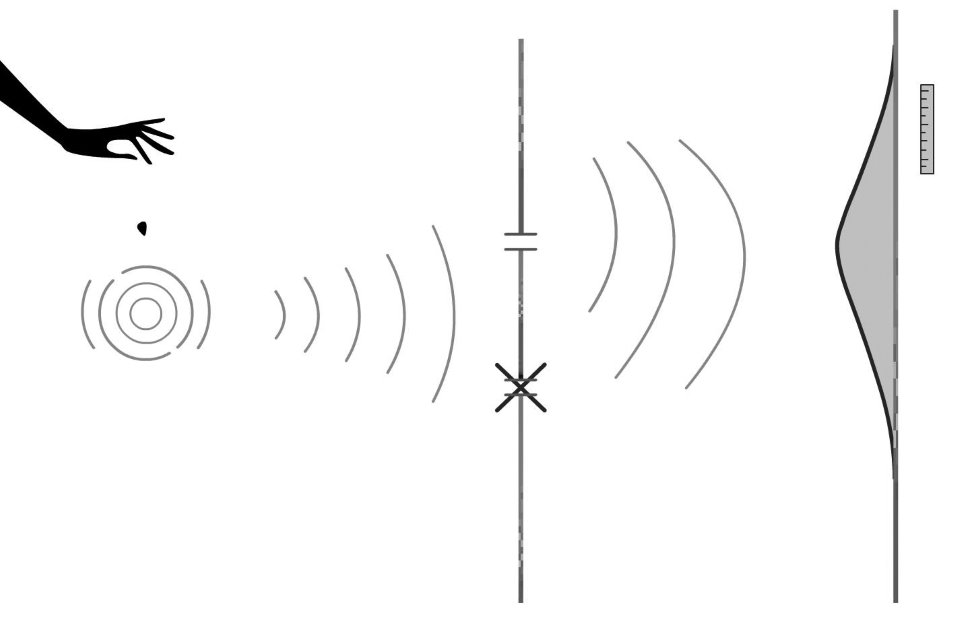
איור א 3: ניסוי שני החריצים בגלים, חריץ אחד פתוח
איור א 4: ניסוי שני החריצים בגלים, שני החריצים פתוחים
כך לחלופין ישנן נקודות דומות לנקודה a ונקודות דומות לנקודה b, ההתאבכות בונה והורסת לחלופין. כל מי ששיחק אי פעם במערכות שמע יודע שאם נעמיד שני רמקולים בקצוות החדר ונזין לשניהם אות שמע זהה, נקבל בחדר נקודות שבהן השמע חזק יותר או חלש יותר לחלופין, זו בדיוק התופעה של התאבכות שני מקורות הגל.
אם עדיין לא השתכנעתם תוכלו לצייר את שיאי הגלים המגיעים מכל אחד מהחריצים בדיוק כמו באיור א4, ולוודא שנקודה b לא נמצאת על חיתוך של שני קווים כאלו אלא על חיתוך של גל אחד ובין שני שיאים של הגל השני.
כעת לחלק המדהים של הסיפור שלנו. נעשה את הניסוי הזה בתווך אחר. התותח שלנו יהיה תותח היורה אלקטרונים,10 הגלאי שלנו יהיה גלאי אלקטרונים. נראה לכאורה שחזרנו למקרה הראשון של תותח היורה כדורים, אומנם קטנים אבל בכל זאת כדורים. נבדוק את תוצאות הניסוי. אם נחסום את אחד החריצים כגון החריץ התחתון, נקבל תוצאה הדומה לזו שבאיור א1. מה יקרה כעת אם נפתח את שני החריצים? אנחנו מצפים לתוצאה הדומה לזו שבאיור א2, שהיא סכום של שתי האמפליטודות. להפתעתנו נגלה שפתיחת שני החריצים נותנת לנו תבנית של התאבכות על גבי הקיר הסופג, כמו בתוצאה של גלים. כיצד ייתכן הדבר? הרי הניסוי נערך בחלקיקים? כיצד ייתכן שהניסוי נעשה בחלקיקים והתוצאה שהתקבלה היא תוצאה של גלים?
ננסה להבין את המוזרות. נתבונן למשל בנקודה b באיור א4, כעת שני החריצים פתוחים. בנקודה זו, לו החריץ התחתון היה סגור היינו מקבלים יותר אלקטרונים (ראה למשל את אותה נקודה באיור א1). כאשר החריץ התחתון פתוח נקבל שם פחות אלקטרונים. כלומר פתחנו אפשרות נוספת לאלקטרונים להגיע לנקודה זו (פתחנו את החריץ התחתון) וקיבלנו פחות אלקטרונים. נניח לדוגמה שבכיתת סטודנטים ישנן שתי דלתות יציאה ומישהו עומד מחוץ לכיתה במרחק מה מהדלתות וסופר כמה סטודנטים מגיעים אליו. אפשר לשחרר את הסטודנטים להפסקה ולפתוח רק דלת אחת ואפשר לפתוח שתי דלתות. נראה לנו ברור מאוד שאם שתי הדלתות ייפתחו יגיעו אל המודד יותר סטודנטים מאשר אם רק דלת אחת תיפתח.
מה קורה אם כן במקרה של האלקטרונים? הסבר אחד יכול להיות שהאלקטרונים מפריעים זה לזה כאשר שני החריצים פתוחים. אנחנו יכולים לוודא שדבר כזה לא יקרה אם נשגר את האלקטרונים אחד אחד ונחכה מספיק זמן כך שלא ייווצר מצב שבו שני אלקטרונים נמצאים בעת ובעונה אחת בניסוי. ואולם מסתבר שגם אם נקפיד על הפרדה מוחלטת, נקבל בדיוק את אותן התוצאות. בנקודה b מגיעים פחות אלקטרונים כאשר שני החריצים פתוחים. זה נראה כבר ממש כמו קנוניה של הטבע. האלקטרונים אשר היו אמורים להגיע ל-b כשהחריץ התחתון סגור, יודעים שהחריץ הזה פתוח כעת ולכן מחליטים לא להגיע ל-b (אפשר אפילו לפתוח את החריץ רק לאחר שהאלקטרון כבר יצא למסלולו). העובדה שהם אמורים להגיע לנקודה b נקבעת במסלול שלהם עוד בנקודת הפתיחה. כלומר מכל תנאי ההתחלה המצויים כאשר תותח האלקטרונים יורה אותם, הזווית, העוצמה, הכיוון וכל שאר תנאי ההתחלה, אלו יקבעו אם החלקיקים יעברו לדוגמה דרך החריץ העליון ומשם לנקודה b. כעת נודע להם שהחריץ התחתון נפתח והם משנים את דעתם ובוחרים להגיע למקומות אחרים ולהימנע מנקודה b.
בכל דרך שננסה להסביר את התופעה נגיע לאבסורד, לא ייתכן שלחלקיקים ישנו סוג של מודעות למה שקורה בניסוי.
יש דרך אחת להיחלץ מכל זה, והיא לשנות לחלוטין את כללי המשחק. אנחנו יכולים להחליט שמדובר כאן בגלים ולא בחלקיקים. האלקטרון המשתתף בניסוי הופך פתאום לגל. זה יסביר מייד את התוצאות, שכן אלו תוצאות סבירות בניסוי של גלים. אנו נראה שהחלטה כזאת פותחת תיבת פנדורה שלמה מלאה בבעיות שננסה לגעת בהן בספר זה.
מהי המשמעות של שינוי התפיסה שלנו של מהות האלקטרון, וכיצד ייתכן שניסוי פשוט גורם לנו לשנות את תפיסתנו את האונטולוגיה שבטבע?
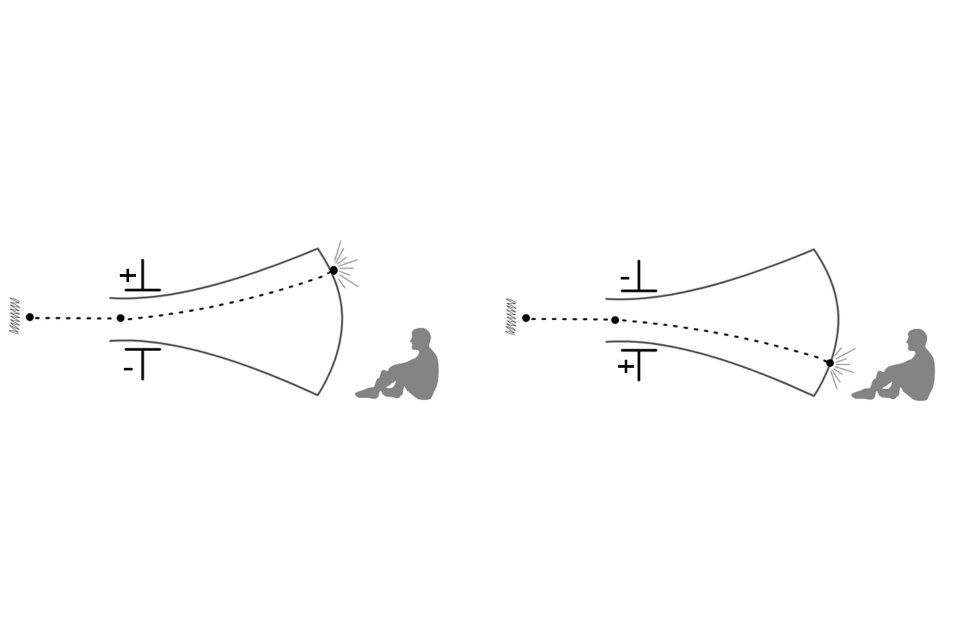
התובנה שלנו שאלקטרונים הם חלקיקים בנויה על מסורת ארוכה של ניסויים שבהם האלקטרון התנהג כמו חלקיק. אם נעביר אלקטרון בשפופרת קרן קתודית,11 כמו זו של טלוויזיה ישנה (איור א5), נגלה שהאלקטרון מושפע מכוחות חשמליים ומגנטיים. נוכל להציב בשפופרת או מסביבה מגנטים או לוחות אלקטרודות, לשנות את השדה המגנטי והחשמלי ולהבחין שהאלקטרון מתנהג תחת הכוחות האלו כאילו הוא כדור קטן שטעון במטען חשמלי. על סמך ניסויים כאלו התקבלה אצלנו התחושה שהאלקטרון הוא חלקיק. כעת מתקבלת אצלנו תחושה שונה שהאלקטרון הוא גל.
נוכל אולי לומר שאלקטרון הוא גם חלקיק וגם גל. אם מתבוננים בו בניסוי שני החריצים הוא מגלה את תכונות הגל שלו, ואם מתבוננים בו בניסוי שפופרת הקרן הקתודית הוא מגלה תכונות של חלקיק. אם כן לאלקטרון ישנן תכונות התלויות בניסוי שעושים. זה נשמע מוזר. אנחנו לא מכירים תופעות קלסיות כאלו. החלקיקים הקלסיים שאנו מכירים לא משנים את מהותם בשל ניסוי שנעשה בהם. כל מטרתו של הניסוי הוא לבדוק תכונה שקבועה בהם אפריורית. הניסוי רק נועד לחשוף תכונה כזו. כאן נראה לכאורה שהניסוי קובע בסופו של דבר את מהותו של החלקיק. אנחנו נגלה הרבה פנים לטענה זו בהמשך הדיון.
האלקטרונים כאן הם רק דוגמה לחלקיקים ברמה אטומית, נקרא להם חלקיקים קוונטיים, ואם כך כל החלקיקים הקוונטיים הם גלים. ואולם מהו התווך של אותם גלים? אנו מכירים גלים בתוך מים או גלי קול. מהו התווך של הגלים כאן? הרי הניסוי לא נעשה בתוך מים או בתווך אחר.
איור א5: שפופרת קרן קתודית
הגלים במים הם לא יותר מאשר שינויים בתוך התווך, שינויים הניצבים לכיוון התקדמות הגל. בבריכת מים הגלים הנראים הם שינויים למעלה ולמטה בגובה פני המים בעוד שהגל מתקדם במאונך לשינויים, כלומר על פני המים. בגל קול ישנם שינויים בדחיסוּת של האוויר והגל מתקדם בכיוון דומה לשינויים בדחיסות. בפיזיקה הקלסית מושג הגל מופיע בהכרח בצמוד לתווך. הגל הוא לא יותר מאשר שינויים או הפרעה המתקדמת בתווך, הוא לא התקדמות התווך אלא התקדמות הפרעה כלשהי בתווך. אם ניקח קפיץ גדול מאוד, נחבר אותו לצד אחד של קיר החדר, נחזיק בצד השני ונבקש מחבר להצמיד חלק מכריכות הקפיץ במקום מסוים על גביו ואז לשחרר את אחיזתו מהן, נוכל לראות כיצד ההפרעה על גבי הקפיץ מתקדמת לאורכו עד לקיר ואולי אף חוזרת ממנו. ברור שאף לא אחת מכריכות הקפיץ זזה ממקומה אל עבר הקיר וחזרה, אלא שההפרעה התקדמה בתוך הקפיץ, הדחיסות השתנתה במקום מסוים וההפרעה הזאת בדחיסות התפשטה. אם כן גל הוא הפרעה שמתקדמת בתווך כלשהו. מהו הגל במקרה שלנו?
בניסוי שלנו עם האלקטרונים אין לנו תווך ששינויים בו יכולים להוות גל. בתורת היחסות מסתבר שגלים כמו גלים אלקטרומגנטיים לא צריכים תווך כדי להתפשט בו, ואולם שם היה לנו מושג של שדה, הגלים האלקטרומגנטיים הם הפרעות בתוך השדה האלקטרומגנטי. אם כך מה מהותו של הגל כאן? הפרעה בתוך איזה תווך או שדה?
נראה לנו לכאורה שהגל המופיע כאן הוא גל וירטואלי. אנחנו יכולים להשתמש בו כסוג של ארטיפקט מתמטי (מודל, או יצירה מלאכותית מתמטית) שנועד אך ורק כדי לעזור לנו לחשב את התבנית או את ההסתברויות לקבלת אלקטרון במקום כזה או אחר על גבי הקיר הסופג. נוכל לדמיין שיש כאן גלים שיוצאים משני החריצים, נוכל לחשב את ההתאבכות הצפויה משני גלים כאלו ואז לחשב את ההתפלגות12 הנכונה של החלקיקים, כל זאת מבלי להאמין בקיום ממשי של הגל. ישנו כלי מתמטי אשר עוזר לנו לחשב את התפלגות האלקטרונים על גבי הקיר הסופג. טענה כזאת היא מוזרה במקצת, אנו משתמשים בסוג של מטפיזיקה13 כדי להקל עלינו את התיאור הפיזיקלי. ככל שנתעמק יותר בפיזיקה הקוונטית נקבל את התחושה שלגל כזה בהחלט קיימת ממשות מעבר להיותו כלי מתמטי, הוא אכן חלק מהפיזיס (הטבע, מה שמתארת הפיזיקה). בינתיים נכנה אותו גל הסתברות.
נסיים בשאלה מעט פילוסופית: אם הטבע בנוי מגלים, כיצד ייתכן שאנחנו רואים גופים ממשיים כמו שולחן, מחשב וכולי. שאלה זו תעסיק אותנו בפרק הבא.